Binary Search :
An advanced-level algorithm for locating a target in a sorted array is efficient, precise, and can be optimally executed through binary search. A target value is located by comparing it to a centre value, and subsequently discarding one-half of the remaining elements.
Use case for binary search:
- Iterative Binary Search Code Example
- Amount of resources utilised over time
- Handling overflow issues
- When duplicates exist, and you need the first or last index.
Important to consider:
Information is organized for ease of access. It is imperative to note that binary search requires a certain degree of skill and practice in identifying the best methods for locating precise information in an orderly manner.
As binary search combines methodical elimination with dividing the search area, it is easier to locate the desired element faster.
Algorithm:
Here is how we will implement the binary search algorithm on the given array:

Step 1: Split the range into 2 parts:
To split the range, we need the bound ‘mid’ to do the following:
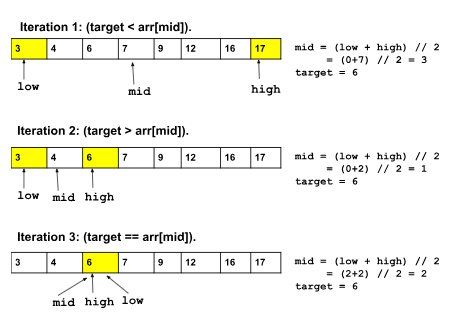
mid = (low+high) // 2 bounds both sides of the range (‘//’ is the sign for floor division)
Step 2: On this step we will relate the middle value to the target:
During this step we can notice 3 different alternatives arising:
If arr[mid] equals to target: This means that the value we were looking for have encountered already in the earlier step. So, in this step, we can straight way provide the index of the target without any further evaluation.
If target is greater than arr[mid]: This case tells us that our target exists in the other half of the array, hence for this case the new range will be upper half.
If target is lesser than arr[mid]: This case gives the conclusion that our target exists in the lower half of the array. In this case, the new range will be lower half.
Step 3: Reduce The Search Space
We will now narrow the search area according to the probable position of the target.
If the target is to the left, we will set high pointer to mid -1; therefore, the left half will be the next search space.
If we suppose that the target occurs on the right, we will set the low pointer to mid +1; therefore, the right half will be the next search space.
Iterative implementation:
1. Pointer low will be 0 and high will be n-1 (where n = size of the given array) at the start.
2. Now, we will do all the three steps explained before in the algorithm section in a loop.
3. The loop will continue until we find the target, or either of the pointers cross each other.
Example :

